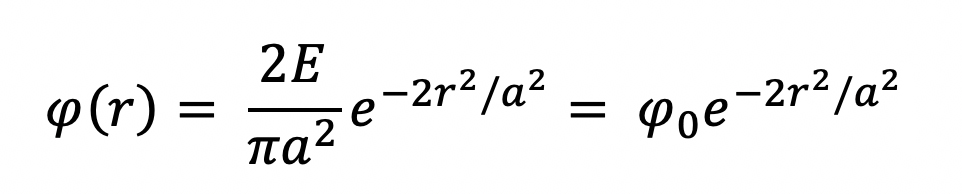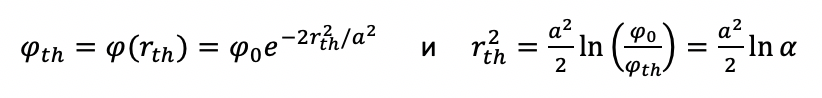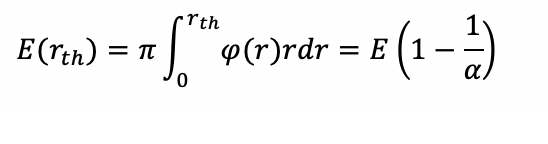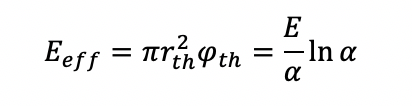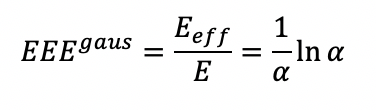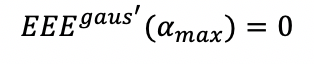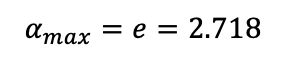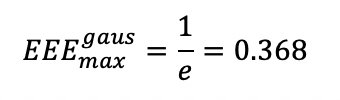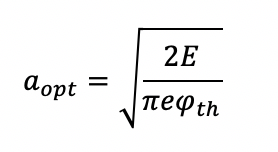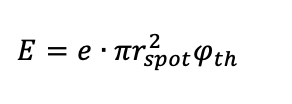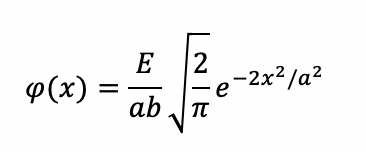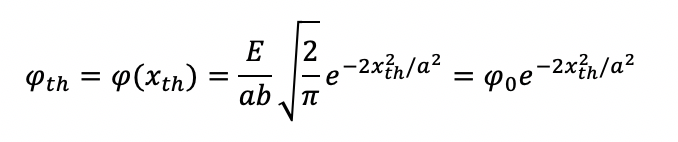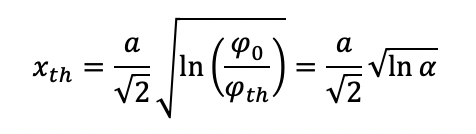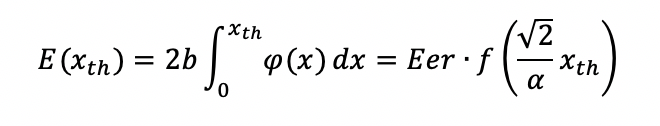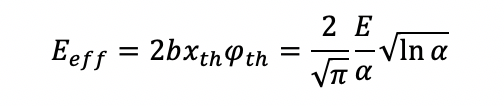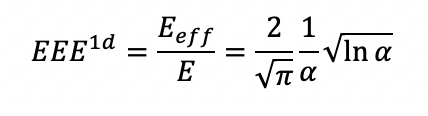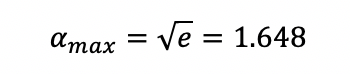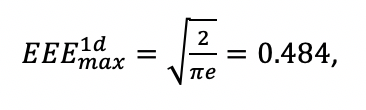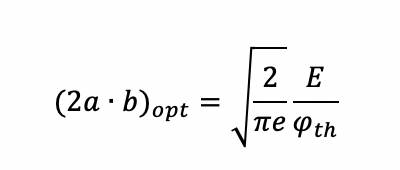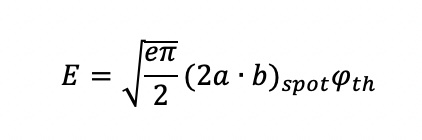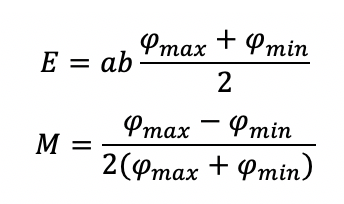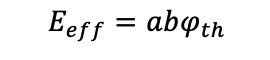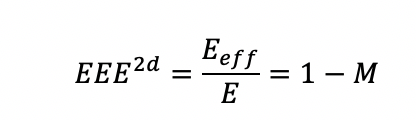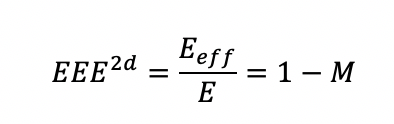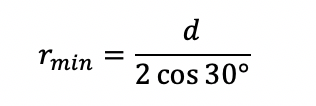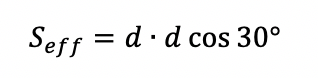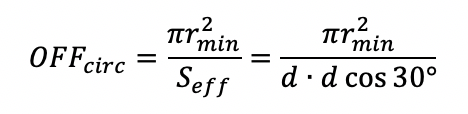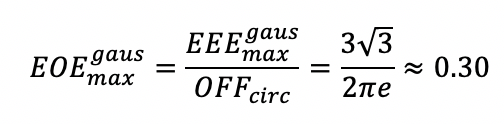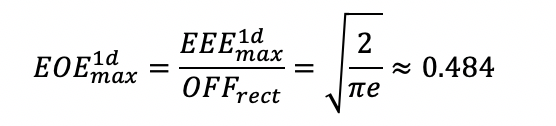Абляция тонкопленочных слоев с помощью лазеров с различными профилями пучка: энергоэффективность и коэффициент заполнения

Тонкие пленки играют все более важную роль в современном обществе. Структурирование и формирование рельефа тонкого слоя с помощью селективной лазерной абляции является одной из ключевых технологий в производстве дисплеев и фотоэлектрических элементов. Двумя основными аспектами тонких пленок являются образование тонкой пленки и структурирование или модификация тонкой пленки. Поэтому лазерное излучение, благодаря его пространственной фокусируемости и временной управляемости, все чаще используется для структурирования и модификации тонких пленок.

Одновременно в производстве тонкопленочных солнечных элементов используются два процесса абляции: скрайбирование с помощью селективной абляции и технологическая изоляция с помощью удаления кромки. Для уменьшения потерь солнечный активный слой сегментируется по зонам. Активные зоны соединяются последовательно посредством гомогенного процесса осаждения из паровой фазы и процесса скрайбирования по очереди. Для электрической изоляции и герметизации солнечных элементов все слои в граничной области полностью обработанных солнечных элементов на стеклянной подложке должны быть удалены. Ввиду огромного потенциального применения процесс лазерной абляции также интенсивно исследуется для скрайбирования и структурирования тонких пленок на кремниевых подложках [1, 2, 3].

Обычные лазерные пучки имеют круглое поперечное сечение. Кроме того, большинство современных лазеров высокого качества имеют гауссов профиль пучка. Из-за порогового поведения гауссов профиль пучка не благоприятен для процесса абляции [1, 2, 3]. Появление концепции лазеров с технологией InnoSlabпозволяет получать пучок с одномерным линейным профилем с плоской вершиной и с высоким качеством [4, 5, 6, 7]. Одномерный линейный профиль может быть преобразован в круговой гауссов или в двумерный с квадратным или прямоугольным поперечным сечением. В этой статье мы обсудим основы процессов абляции со следующими профилями пучка: круговой гауссов, одномерный линейный с плоской вершиной и двумерный квадратный с плоской вершиной. Основными вопросами будут энергетическая эффективность процесса и коэффициент заполнения для различных профилей пучка. Соответствующие экспериментальные результаты будут представлены.

Эффективная энергоэффективность (EEE)

Пучок с круговым гауссовым профилем

Рассмотрим круговой гауссов пучок с энергией импульса E. Он сфокусирован вниз до точки с радиусом a на поверхности образца. Тогда плотность потока φ(r) кругового гауссова пучка определяется по формуле:

 

где φ₀ = 2E/πa² – максимальная плотность потока на оси.

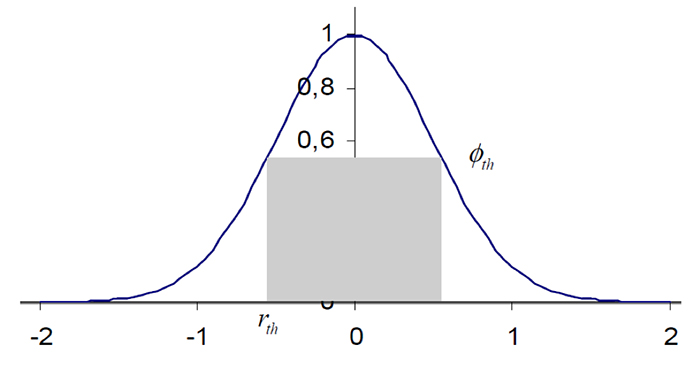
Учитывая пороговую плотность потока для процесса абляции φ_th, мы имеем:

где r_th – радиус с пороговой плотностью потока, а α = φ₀/φ_th – отношение максимальной плотности к пороговой плотности потока.

Энергия внутри круга r_th определяется интегралом плотности потока:

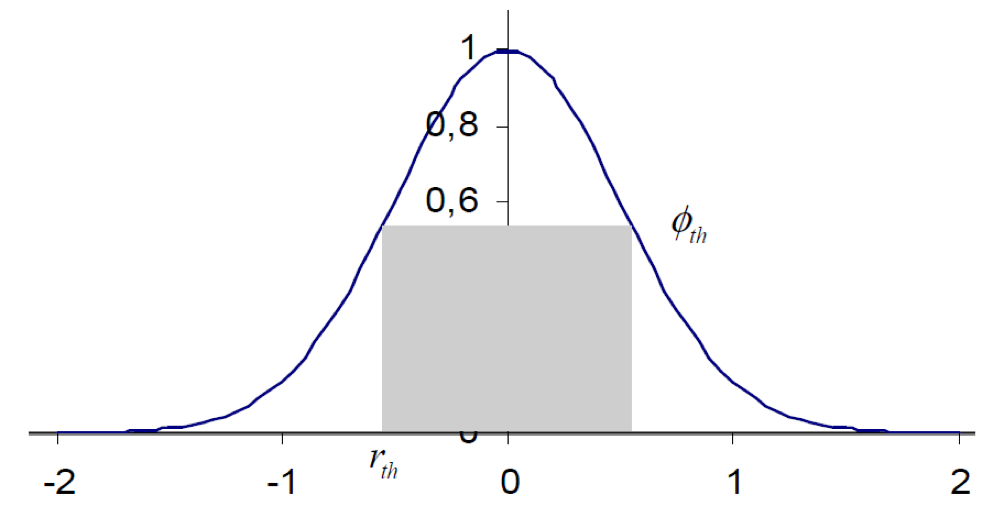
Рис. 1. Распределение плотности потока в луче с гауссовым профилем.

Как показано на рис. 1, эффективная энергия процесса, полезная для абляции, является произведением площади диска, определяемой как r_th, и пороговой плотности потока φ_th:

Для того, чтобы охарактеризовать эффективность процесса абляции, мы определяем эффективную энергоэффективность как отношение эффективной энергии процесса к полной энергии:

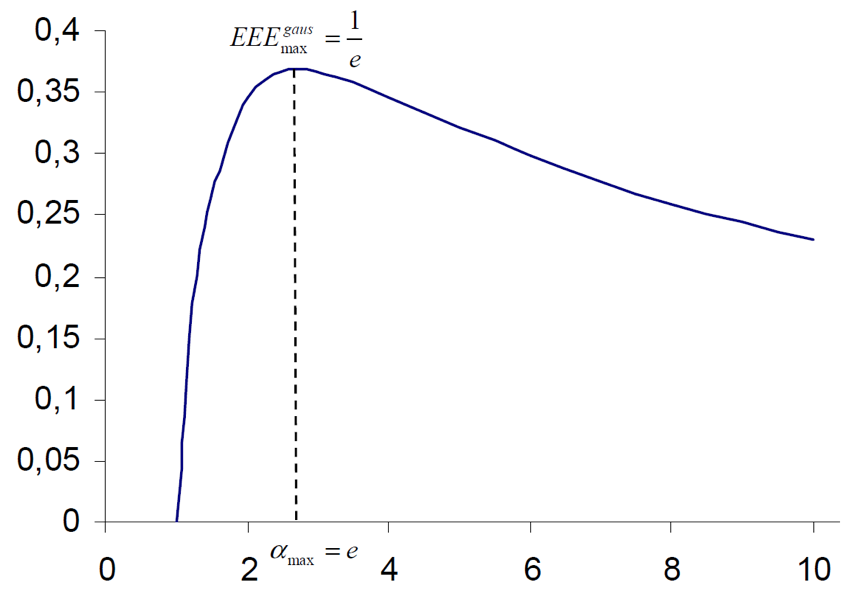
На рис. 2 показана зависимость эффективной энергоэффективности от отношения плотностей потока: сначала эффективная энергоэффективность увеличивается, а после достижения максимума начинает уменьшаться с увеличением отношения плотностей потока.

Рис. 2. Зависимость эффективной энергоэффективности от отношения плотностей потока для кругового гауссова профиля.

Существует максимальное значение эффективной энергоэффективности, определяемое как:

и достигается, когда отношение максимальной плотности к пороговой плотности потока равно:

Соответствующий максимум эффективной энергоэффективности в этом случае будет равен:

Это означает, что только 36.8% энергии максимально полезны для процесса абляции. Другая часть энергии импульса является потерянной энергией и не способствует процессу абляции. Что еще хуже, потерянная энергия нагревает подложку и приводит к нежелательному эффекту и влиянию на подложку.

В случае заданного порога и энергии импульса оптимальный радиус пучка для получения максимальной эффективной энергоэффективности определяется по формуле:

В случае заданного порога и размера пятна для абляции, требуемую энергию импульса можно рассчитать как:

Пучок с одномерным линейным профилем с плоской вершиной

Далее мы обсудим процесс абляции с использованием гауссова пучка с одномерным линейным профилем с плоской вершиной. Для одномерного гауссовского пучка с плоской вершиной с энергией импульса E, длиной b и шириной 2a пространственное распределение плотности потока определяется как:

Для пороговой плотности потока I_th мы имеем:

где φ₀ = E/ab·√(2/π) – это максимальная плотность потока в точке x_th

где α = φ₀/φ_th – отношение максимальной плотности к пороговой плотности потока.

В этом случае энергия в области шириной 2x_th определяется как:

Тогда эффективная энергия процесса, полезная для абляции:

А эффективная энергоэффективность для одномерного гауссовского пучка с плоской вершиной равна

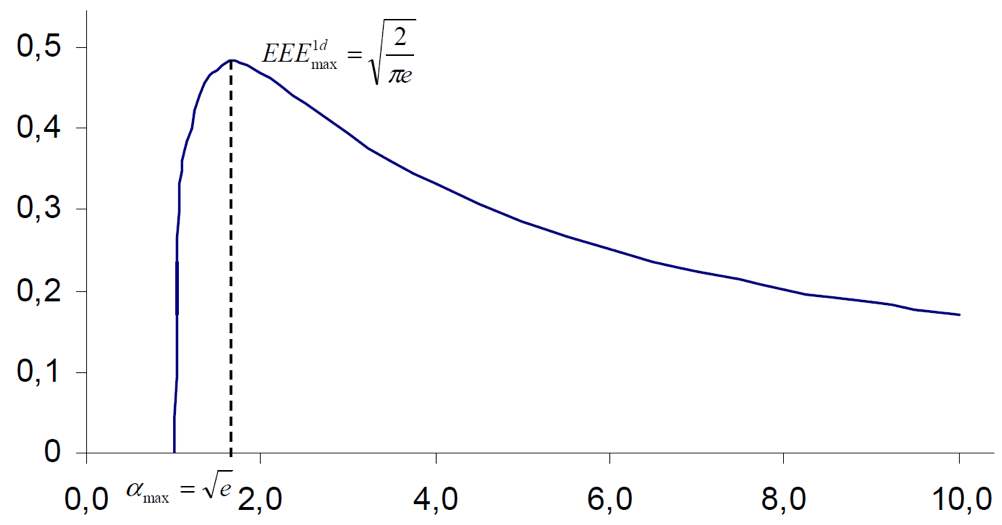
На рис. 3 показана зависимость эффективной энергоэффективности от отношения плотностей потока. Зависимость аналогична пучку с круговым гауссовым профилем: сначала эффективная энергоэффективность увеличивается, а после достижения максимума начинает уменьшаться с увеличением отношения плотностей потока.

Рис. 3. Зависимость эффективной энергоэффективности от отношения плотностей потока для одномерного гауссовского пучка с плоской вершиной.

Максимальное значение эффективной энергоэффективности достигается, когда отношение максимальной плотности к пороговой плотности потока равно:

Соответствующий максимум эффективной энергоэффективности в этом случае будет равен:

что означает, что 48.4% энергии максимально полезны для процесса абляции. Другая часть энергии импульса является потерянной энергией и не способствует процессу абляции. Что еще хуже, потерянная энергия нагревает подложку и приводит к нежелательному эффекту и влиянию на подложку.

В случае заданного порога и энергии импульса оптимальный размер поперечного сечения пучка (2a·b)opt для получения максимальной эффективной энергоэффективности определяется по формуле:

В случае заданного порога и размера пятна для абляции, требуемую энергию импульса можно рассчитать как:

Пучок с двумерным профилем с плоской вершиной

Теперь рассмотрим процесс абляции с использованием пучка с двумерным профилем с квази-плоской вершиной. Интенсивность излучения имеет в основном периодическое изменение с максимальной плотностью потока φmax и минимальной плотностью потока φ_min. Тогда энергия импульса E и модуляция интенсивности M определяются следующими выражениями:

Для абляции тонкой пленки минимальная плотность потока должна быть эквивалентна пороговой плотности потока. В этом случае эффективная энергия процесса, полезная для абляции равна

При этом эффективная энергоэффективность для двумерного гауссовского пучка с квази-плоской вершиной равна

Таким образом, в случае идеального двумерного пучка без модуляции эффективная энергоэффективность составляет 100%.

Коэффициент заполнения (OFF)

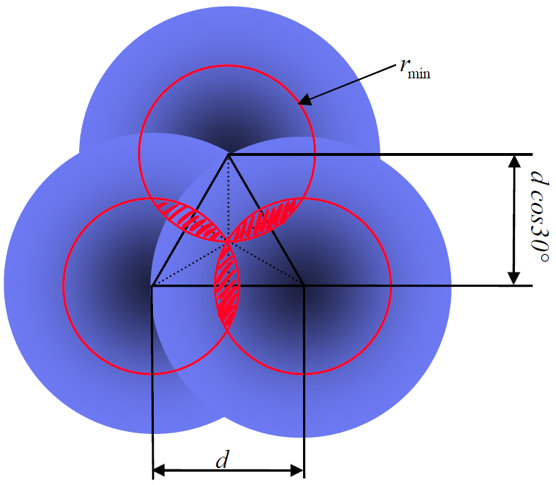
На рис. 4 показано, как область обработки может быть оптимально заполнена пучком круглого поперечного сечения. Для полной абляции существует следующая зависимость между минимальным пороговым радиусом и расстоянием двух лазерных пятен:

Рис. 4. Заполнение области обработки пучком круглого сечения.

Максимальное расстояние между рядами обработки равно d·cos30°, а эффективная площадь на один лазерный импульс определяется как S_eff:

Коэффициент заполнения представляет собой отношение площади, определяемой пороговым радиусом, к эффективной площади на лазерный импульс. Для пучка с круглым поперечным сечением коэффициент заполнения равен:

Очевидно, что для всех пучков с прямоугольным или квадратным поперечным сечением коэффициент заполнения равен единице: OFF_rect = 1

Общая эффективная эффективность (EOE)

Общая эффективная эффективность процесса абляции определяется отношением эффективной энергоэффективности (EEE) к коэффициенту наполнения (OFF).

Для кругового гауссова пучка максимальная EOE определяется как:

Для одномерного пучка с плоской вершиной максимальная EOE определяется как:

Для двумерного пучка с идеальной плоской вершиной общая эффективная эффективность равна единице: EOE^2d = 1.

Заключение

Были представлены основы процессов абляции с использованием лазерных пучков с различными профилями интенсивности и поперечного сечения. Для характеристики эффективности энергии импульса для процессов абляции были введены понятия эффективной энергоэффективности (EEE) и общей эффективной эффективности (EOE). Также были приведены зависимости EEE и EOE от параметров лазерного излучения для пучка с круговым гауссовым профилем, для одномерных пучков с плоской вершиной и для двумерных квадратных пучков с плоской вершиной. Результаты показывают, что круговой гауссов пучок с максимальной общей эффективной эффективностью в 30% является наиболее неэффективным для процесса абляции. Максимальная общая эффективная эффективность одномерного пучка составляет 48%. Двумерный же пучок без учета модуляции имеет 100%-ую общую эффективную эффективность и является наиболее оптимальным выбором для процессов тонкопленочной абляции. Также ожидается самое низкое влияние потерянной энергии во время процесса абляции при использовании двумерных квадратных пучков с плоской вершиной.

Подробные характеристики
Лазера InnoSlab серии BX

Подробные характеристики
Лазера InnoSlab серии IS

Подробные характеристики
Лазера InnoSlab серии GX

Ссылки

P. Engelhart, Lasermaterialbearbeitung als Schlüsseltechnologie zum Herstellen rückseitenkontaktierter Siliciumsolarzellen, PhD Dissertation, Fakultat fur Elektrotechnik und Informatik der Gottfried Wilhelm Leibniz Universitat Hannover, June 2007

P. Engelhart, S. Hermann, T. Neubert, R. Grischke, N.-P. Harder, R. Brendel, Laser processing for high efficiency solar cells, Proceeding of 17th NREL-Workshop, 1 903 (2007)

S. Haas, S. Ku, G. Schöpe, K.-M. Du, U. Rau, H. Stiebig , Patterning of thin-film silicon modules using lasers with tailored beam shapes and different wavelengths, Proc. 23rd European Photovoltaic Solar Energy Conference Valencia, Spain, September 2008

K.-M. Du, N.-L. Wu, J.-D. Xu, J. Giesekus, P. Loosen, and R. Poprawe, Partially end-pumped Nd:YAG slab laser with a hybrid resonator, Opt. Lett. 23, 370 (1998)

K.-M. Du, D.-J. Li, H.-L. Zhang, P. Shi, X.-Y. Wei, and R. Diart, Electro-optically Q-switched Nd:YVO4 slab laser with a high repetition rate and a short pulse width, Opt. Lett. 28, 87 (2003)

P. Zhu, D.-J. Li, B.-S. Qi, A. Schell, P. Shi, C. R. Haas, S.-J. Fu, N.-L. Wu, and K.-M. Du, Diode end-pumped high-power Q-switched double Nd:YAG slab laser and its efficient near-field second-harmonic generation, Opt. Lett. 33, 19 (2008)

D.-J. Li, Z. Ma, C. R. Haas, A. Schell, J. Simon, R. Diart, P. Shi, P.-X. Hu, P. Loosen, and K.-M. Du, Diode-pumped efficient slab laser with two Nd:YLF crystals and second-harmonic generation by slab LBO, Opt. Lett. 32, 10 (2007)